1° Ano do Ensino Médio e Técnico

Caros alunos!!!
Conforme combinado postarei no blog materiais que serão utilizados em aula.
Att, Prof Diego

Fórmulas de Física. Baixar

Índice da Página

1. O que é Cinemática?
2. Movimento Retilíneo Uniforme (MRU)
3. Função Horária da Posição do MU
4. Gráficos do MRU
5. Movimento Retilíneo Uniformemente Variado (MRUV)
6. Aceleração Média
7. Função Horária da Velocidade
8. Função Horária da Posição do MRUV
9. Equação de Torricelli
10. Simulados sobre Movimento Retilíneo Uniformemente Variado
11. Movimento de Queda Livre
12. Simulado sobre Movimento de Queda Livre
13. Vetor
14. Força
15. 1° Lei de Newton
16. 2° Lei de Newton
17. Força Peso
18. Força Elástica
19. Força de Atrito
20. Força Centrípeta
21. 3° Lei de Newton
22. Plano Inclinado
23. Sistema de Blocos
24. Trabalho de uma Força
25. Potência
26. Rendimento

CINEMÁTICA

É um importante ramo da Mecânica e é responsável por descrever o movimento dos corpos sem se preocupar com suas causas.

CONCEITOS FUNDAMENTAIS DA CINEMÁTICA ESCALAR

O QUE É CINEMÁTICA ESCALAR?

Cinemática Escalar é um dos principais ramos da Mecânica. Trata-se da área que estuda o movimento dos corpos sem atribuir-lhes uma causa. A palavra escalar refere-se ao fato de lidarmos com movimentos unicamente unidimensionais, ou seja, que se desenvolvem unicamente ao longo de uma direção do espaço, dispensando, dessa forma, o tratamento vetorial das grandezas físicas envolvidas.

Para o estudo da Cinemática Escalar, alguns conceitos são de grande importância, portanto, trataremos aqui daqueles que são fundamentais para o seu entendimento.

Corpo: É uma porção limitada de matéria e é constituído por partículas, mas pode ser tratado macroscopicamente como um único corpo no âmbito da Cinemática Escalar.

Ponto material: É todo corpo cujas dimensões podem ser desprezadas em relação às distâncias envolvidas.

Corpo extenso: É todo corpo cujas dimensões são comparáveis às escalas envolvidas. Nesse caso, elas não podem ser desprezadas.

Referencial: É o sistema de referência adotado. A partir dele, são medidas as distâncias, larguras, profundidades etc. O referencial é a posição do espaço ocupada pelo observador.

Posição: É o espaço ocupado por um corpo e é determinado pela distância medida em relação a algum referencial.

Repouso: Sempre que um corpo mantiver sua posição constante em relação a algum referencial, diremos que esse corpo encontra-se parado em relação a ele.

Movimento: Quando a posição de um corpo mudar em relação a um dado referencial, diremos que esse corpo encontra-se em movimento em relação a esse referencial.

Trajetória: É a sucessão das posições ocupadas pelo corpo em relação a um dado referencial.

Deslocamento (ΔS): É a diferença entre a posição inicial (S0) e a posição final (S) de um corpo em relação a algum referencial. Em movimentos cíclicos ou em trajetórias fechadas, o deslocamento será sempre nulo.
É definido por:

Espaço percorrido: É a soma dos módulos de todas as distâncias percorridas durante um movimento.

MOVIMENTO RETILÍNEO UNIFORME (MRU)

Velocidade Média (Vm)

É a razão da variação da posição ou deslocamento (ΔS) pelo intervalo de tempo (Δt) de determinado movimento. É definida pela equação:

Velocidade instantânea: É a velocidade apontada pelo velocímetro dos automóveis. É uma velocidade média, mas para intervalos de tempo muito pequenos, próximos de zero.

É todo movimento no qual a velocidade instantânea é sempre igual à velocidade média; nesse caso, dizemos que o móvel percorre distâncias iguais em intervalos de tempo iguais.

Função Horária da Posição do MU

É uma equação matemática de 1º grau utilizada para descrever a posição (S) de um móvel em relação a algum referencial (S0) em função do tempo decorrido (t). É definida pela equação a seguir:

Movimento progressivo: É um movimento no qual a distância aumenta em relação a algum referencial, ou seja, quando estiver afastando-se. Nesse caso, a velocidade tem módulo positivo.

Movimento regressivo ou retrógrado: É um movimento no qual a distância de um móvel em relação a algum referencial diminui. A velocidade no movimento retrógrado é negativa.

Gráficos do MRU

Sabe-se que o movimento de um corpo pode ser definido por uma expressão matemática, por uma tabela ou também por uma representação gráfica. A forma gráfica é muito importante pois pode fornecer muitos detalhes de um movimento, ou ainda, facilitar a comparação de movimentos de corpos diferentes.

Gráfico v Vs t

No movimento uniforme, a velocidade é constante e o diagrama da velocidade em função do tempo v = f(t) é uma reta paralela ao eixo dos tempos.

É importante observar, que a área (A) compreendida entre o gráfico e o eixo dos tempos é numericamente igual ao valor do deslocamento do corpo.

Gráfico S Vs t

Ao observar que a função horária do espaço no movimento uniforme é do 1º grau (S = So + v.t), conclui-se que o gráfico S Vs t é uma reta inclinada.
Se o movimento é progressivo, a reta é crescente ou inclinada para cima;

Se o movimento é retrógrado, a reta é decrescente ou inclinada para baixo;

É fácil observar no gráfico que a posição inicial do móvel é indicada pelo ponto em que a reta corta o eixo das ordenadas (eixo S) e que a declividade da reta representa a velocidade escalar do móvel:

MOVIMENTO RETILÍNEO UNIFORMEMENTE VARIADO (MRUV)

Também conhecido como movimento acelerado, consiste em um movimento onde há variação de velocidade, ou seja, o móvel sofre aceleração à medida que o tempo passa.

Mas se essa variação de velocidade for sempre igual em intervalos de tempo iguais, então dizemos que este é um Movimento Uniformemente Variado, ou seja, que tem aceleração constante e diferente de zero.

Aceleração Média

Aceleração média é a relação entre a velocidade de uma partícula e o intervalo de tempo correspondente.

A unidade da aceleração no S.I é o metro por segundo ao quadrado (m/s²).

Exemplos:

1) Calcule a aceleração média de um carro, sabendo que sua velocidade varia de 4 m/s para 12 m/s em 2 s.

2) Partindo do repouso, um avião percorre a pista e atinge a velocidade de 360 km/h, em 25 s. Qual o valor da aceleração, em m/s²?

Classificação do Movimento

Movimento acelerado: É o movimento em que os sinais da aceleração e velocidade são iguais. Note que nesse movimento o módulo da velocidade aumenta com o tempo.

Movimento retardado: É o movimento em que os sinais da aceleração e velocidade são diferentes. Note que nesse movimento o módulo da velocidade diminui com o tempo.

Função Horária da Velocidade

A função horária da velocidade do Movimento Uniformemente Variado, que descreve a velocidade em função do tempo é dada pela equação abaixo:

Exemplo:
1) A função da velocidade de um móvel em movimento retilíneo é dada por v = 50 + 4t (no SI).
a) Qual a velocidade inicial e a aceleração do móvel?
b) Qual a velocidade do móvel no instante 5 s?
c) Em que instante a velocidade do móvel é igual a 100 m/s?

Função Horária da Posição do MRUV

A melhor forma de demonstrar esta função é através do diagrama velocidade versus tempo (v x t) no movimento uniformemente variado.

Seja So a posição inicial do móvel e Vo a velocidade inicial no instante de tempo to = 0. Considere também S e V como sendo a posição e a velocidade do móvel no instante de tempo t.

Sabendo-se ΔS = S - So que é a área abaixo da curva de v(t) x t e sendo ΔV = V - Vo a velocidade V dado pela equação V = Vo + a.Δt pode-se escrever:

Interpretando esta função, podemos dizer que seu gráfico será uma parábola, pois é resultado de uma função do segundo grau.

Exemplo:

1) Um móvel desloca-se sobre uma trajetória retilínea obedecendo à função S = - 3 - 2t + t² (no SI). Pedem-se:
a) a posição inicial, a velocidade inicial e a aceleração do móvel.

b) a função horária da velocidade desse móvel.

c) a velocidade do móvel no instante 8 s.

d) o instante que o móvel passa pela origem das posições.
Quando o enunciado solicitar o instante/tempo, devemos resolver através da fórmula de Báskara.

Como na Física não utilizamos tempo negativo, a resposta aceitável é 3 s.

Equação de Torricelli

Para o Movimento Retilíneo Uniformemente Variado pode-se relacionar velocidade, aceleração e espaço percorrido isolando-se a variável tempo na equação de velocidade V = Vo + a.Δt e substituindo na equação de posição S = So + Vo.t + (a.t²)/2.

onde obtém-se a equação de Torricelli
Exemplos:

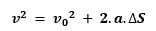
1) Uma bicicleta tem velocidade inicial de 4 m/s e adquire uma aceleração constante de 1,8 m/s². Qual é sua velocidade após percorrer 50 m?

2) Um carro corre a uma velocidade de 72 km/h. Quando freado, para após percorrer 50 m. Calcule a aceleração introduzida pelos freios.

SIMULADO SOBRE ACELERAÇÃO.
SIMULADO SOBRE FUNÇÃO HORÁRIA DA VELOCIDADE.
SIMULADO SOBRE FUNÇÃO HORÁRIA DA POSIÇÃO DO MRUV.
SIMULADO SOBRE EQUAÇÃO DE TORRICELLI.

MOVIMENTO DE QUEDA LIVRE (MQL)

Chamaremos de Queda Livre o movimento de subida ou de descida que os corpos realizam - sujeitos à gravidade nas proximidades da Terra - e desprezaremos as resistências de qualquer espécie.

Os corpos são atraídos pela Terra porque em torno dela há uma região chamada campo gravitacional exercendo atração sobre eles.

No campo gravitacional os corpos são atraídos para a Terra, sofrendo variações de velocidade por terem adquirido aceleração, chamada aceleração da gravidade ou, simplesmente, gravidade, representada pela letra g.

A aceleração com que os corpos caem próximos à superfície da terra é de aproximadamente 9,8m/s².

A aceleração da gravidade é sempre vertical e dirigida para baixo. O valor da aceleração da gravidade varia de ponto para ponto na superfície da Terra e diminui com a altitude.

Galileu Galilei realizou uma série de experiências sobre a queda livre dos corpos e chegou às seguintes conclusões:

Todos os corpos, independentemente de sua massa, forma ou tamanho, caem com a mesma aceleração.

A distância percorrida por um corpo em queda livre é proporcional ao quadrado do tempo gasto para percorrê-la, isto é, a função horária das posições S = f(t) é do 2° grau.

Se a aceleração da gravidade é constante e a função horária das posições é do 2° grau, decorre que a queda livre é um MRUV e, portanto, valem todas as funções e conceitos desse movimento.

Para estudar a queda dos corpos vamos considerar dois tipos de lançamento: Vertical para cima e Vertical para baixo.

Lembrando que um corpo, lançado verticalmente para cima, realiza durante a subida um movimento retilíneo uniformemente retardado, pois o modulo de sua velocidade diminui no decorrer do tempo.

Como dito anteriormente, no movimento de queda livre valem todas as funções do MRUV. Porém há duas pequenas mudanças nas funções.

1° - Onde usávamos a letra a (aceleração) agora usa-se a letra g (aceleração da gravidade).
2° - Onde havia a letra S (distância) agora será a letra h (altura).

Como podemos perceber, o conceito não mudou apenas as letras.

Exemplos:

1) Abandona-se um corpo do alto de uma torre de 80m de altura. Desprezando a resistência do ar e adotando g = 10m/s², determine:
a) o tempo gasto pelo corpo para atingir o solo.

b) a velocidade do corpo ao atingir o solo.

2) Um corpo é lançado do solo verticalmente para cima, com velocidade inicial de 30m/s. Desprezando a resistência do ar e admitindo g = 10m/s², calcule:
a) o tempo gasto pelo corpo para atingir a altura máxima.

b) a altura máxima atingida em relação ao solo.

c) o tempo gasto pelo corpo para retornar ao solo.
Como o corpo retornará para o mesmo local de lançamento, no caso o solo, temos que o tempo de subida é igual ao tempo de descida. Portanto, se ele demorou 3s para subir e ele irá gastar mais 3s para descer, sendo assim ele gastará 6s para retornar ao solo.

d) a velocidade ao chegar ao solo.
SIMULADO SOBRE QUEDA LIVRE.

VETOR

Estudaremos agora os vetores, que são símbolos matemáticos utilizados para representar o módulo, a direção e o sentido de uma grandeza física vetorial.

Podemos, ainda, dizer que vetor é um ente matemático que permite a representação da orientação espacial. A notação de um vetor é feita geralmente utilizando uma letra sobreposta por uma pequena seta, como, por exemplo, ou em NEGRITO.

PROPRIEDADES DO VETOR

MÓDULO: Tamanho, Valor, Quanto ele vale.
DIREÇÃO: Eixo X, Eixo Y ou Eixo Z.
SENTIDO: Positivo ou Negativo.

VETORES UNITÁRIOS

Vetor unitário nada mais é que um vetor igual a 1. Para cada eixo do sistema coordenado, há um vetor unitário.
O vetor unitário aponta para o eixo X, o vetor unitário aponta para o eixo Y e o vetor unitário aponta para o eixo Z.

SOMA ENTRE VETORES

Pode-se obter o vetor resultante através de métodos gráficos (desenhos) e de métodos analíticos (cálculo). Graficamente, têm‐se dois processos: o método do paralelogramo, indicado para soma de dois vetores e o método geométrico, indicado para soma de vários vetores.

A soma ou subtração entre dois vetores será demonimado Vetor Soma, Vetor Resultante ou simplesmente Resultante.

VETORES NO MESMO SENTIDO

Quando os vetores A e B têm a mesma direção e o mesmo sentido, basta somar os dois vetores.

VETORES COM SENTIDO OPOSTO

Quando os vetores A e B têm a mesma direção porém sentido oposto, devemos subtrair os dois vetores.

VETORES PERPENDICULARES ENTRE SI

Quando os vetores A e B apresentam um ângulo de 90° entre si, aplica-se o Teorema de Pitágoras.

VETORES OBLÍQUOS

Quando vetores A e B apresentam um ângulo qualquer, pode-se ser aplicado a Regra do Paralelogramo.

DECOMPOSIÇÃO DE VETOR

Dado um vetor a, podemos encontra outros dois vetores ax e ay tal que ax + ay = a. Vejamos a figura abaixo.

Nesse caso, como ax e ay são vetores perpendiculares entre si, a decomposição é ortogonal. Veja a figura abaixo:

Na figura acima podemos deslocar o vetor ay para a extremidade do vetor ax de modo que o vetor a e seus vetores componentes ortogonais ax e ay formem um triângulo retângulo.

Com base na relação trigonométrica aplicada a um triângulo retângulo, podemos determinar o módulo dos componentes horizontal e vertical do vetor a em função do ângulo θ. Dessa forma, do triângulo amarelo acima temos:

A expressão do módulo do componente horizontal
cos θ = cat adj / hip
cos θ = ax / a
ax = a . cosθ
A expressão do módulo do componente vertical
sen θ = cat op / hip
sen θ = ay / a
ay = a . senθ

DINÂMICA

É o campo da física que estuda as causas dos movimentos e seus efeitos

FORÇA

Quando acontece uma interação entre corpos, podem ocorrer variações na velocidade, deformações ou ambos os fenômenos.

As causas dessas variações ou deformações são denominadas forças.

Quando um corpo é abandonado de uma determinada altura, cai com movimento acelerado devido à força de atração da Terra.

Ao chutarmos uma bola, o pé faz sobre ela uma força que, além de deformá-la, inicia-lhe o movimento.

Quando as superfícies dos corpos que interagem se tocam — como a interação pé — bola, por exemplo —, a força é chamada de contato.

Em Dinâmica vamos tratar de forças cujo efeito principal é causar variações na velocidade de um corpo, isto é, aceleração.

Forças são interações entre corpos, causando variações no seu estado de movimento ou uma deformação.

Tal qual a aceleração, a força é uma grandeza vetorial, exigindo, portanto, para ser caracterizada, uma intensidade, uma direção e um sentido.

A unidade de força no SI é o Newton (N), que será definido mais adiante.

FORÇA RESULTANTE

Seja uma partícula na qual estão aplicadas várias forças. Esse sistema de forças pode ser substituído por uma única força, a força resultante, que é capaz de produzir na partícula o mesmo efeito que todas as forças aplicadas.

EQUILÍBRIO

“Dizemos que uma partícula está em equilíbrio em relação a um dado referencial quando a resultante das forças que ela atua é nula”. Distinguem-se dois tipos de equilíbrio para uma partícula: Equilíbrio Estático e Equilíbrio dinâmico.

Equilíbrio Estático: Um ponto material está em equilíbrio estático quando se encontra em repouso, isto é, sua velocidade vetorial é nula no decorrer do tempo.

Equilíbrio Dinâmico: O equilíbrio é dito dinâmico quando o ponto material está em movimento retilíneo uniforme, isto é, sua velocidade vetorial é constante e diferente de zero.

PRINCÍPIO DA INÉRCIA OU 1° LEI DE NEWTON

Conceito de Inércia: Inercia é a tendência dos corpos em conservar sua velocidade vetorial. Tudo que possui matéria tem inercia. A inércia é uma característica própria da matéria.

Para que as tendências inerciais de um corpo sejam vencidas, é necessário a intervenção de uma força externa.

“Um corpo permanece em repouso ou em movimento uniforme se nenhuma força for exercida sobre ele.
Um corpo livre de uma força externa é incapaz de variar sua própria velocidade”.

A primeira lei de Newton explica por que, quando um ônibus freia bruscamente, os passageiros são projetados para frente. Na freagem, a velocidade do ônibus diminui graças à força dos freios sobre as rodas. Mas os passageiros não são desacelerados. E, por inércia, tendem a se manter em MRU.

PRINCÍPIO FUNDAMENTAL DA DINÂMICA OU 2° LEI DE NEWTON

Massa de um corpo: Podemos associar a massa de um corpo com à sua inércia, dizendo que a massa de um corpo é a medida numérica de sua inércia.

A experiência nos mostra que uma mesma força produzirá diferentes acelerações sobre diferentes corpos. Uma mesma força provoca uma aceleração maior numa bola de tênis do que num automóvel, isto é, quanto maior a massa de um corpo mais força será necessária para produzir uma dada aceleração.

Esse princípio estabelece uma proporcionalidade entre causa (força) e efeito (aceleração).

Se F é a resultante das forças que agem em uma partícula, então, em consequência de F, a partícula adquire, na mesma direção e no mesmo sentido da força, uma aceleração a, cujo módulo é diretamente proporcional a intensidade da força.

A resultante das forças aplicada a um ponto material é igual ao produto de sua massa pela aceleração adquirida.

No Sistema Internacional de unidades (SI) a unidade de massa é o quilograma (kg) e unidade de aceleração é o metro por segundo ao quadrado (m/s²).

Aplicando o princípio fundamental da Dinâmica, temos a unidade de força newton (N).

Um newton (N) é a intensidade da força que, aplicada à massa de 1 kg, produz na sua direção e no seu sentido um movimento de aceleração 1 m/s².

Exemplos:

1) Qual a força aplicada a um bloco de massa 3kg para que ele adquira uma aceleração constante de 2m/s²?

2) Uma força de 50N é aplicada a um corpo de massa 100kg que se encontra em repouso. Sendo esta a única força que atua no corpo, qual a velocidade alcançada após 10s da aplicação da força?

FORÇA PESO

Em torno da Terra há uma região chamada campo gravitacional, na qual todos os corpos sofrem sua influência, que se apresenta em forma de uma força. Essas forças de atração são denominadas forças gravitacionais.

Peso é a força de atração gravitacional que a Terra exerce sobre um corpo.

Desprezando-se a resistência do ar, todos os corpos abandonados próximo à superfície da Terra caem, devido aos seus pesos, com velocidades crescentes, sujeitos a uma mesma aceleração, denominada aceleração da gravidade.

Sendo m a massa do corpo e g a aceleração da gravidade, podemos aplicar o princípio fundamental da Dinâmica e obter o peso P do corpo.

O peso de um corpo é uma grandeza vetorial que tem direção vertical orientada para o centro da Terra e cuja intensidade depende do valor local da aceleração da gravidade.

Em torno de qualquer planeta ou satélite existe um campo gravitacional. Por isso, podemos falar em peso de um corpo na Lua ou em Marte, por exemplo.

A unidade de peso no SI é o newton (N). Podemos ainda utilizar o quilograma-força (Kgf) que é uma unidade de força muito usada pela indústria.

1 Kgf é o peso de um corpo de 1 kg de massa num local em que a aceleração da gravidade é igual a 9,8 m/s².

A relação entre o quilograma-força e o newton é:

Note que peso e massa são grandezas diferentes.
A massa é uma propriedade exclusiva do corpo; não depende do local em que é medida.
O peso do corpo depende do local no qual é medido.

Exemplo:

1) Sobre a superfície da Terra, onde g = 10m/s², um astronauta apresenta peso igual a 700N. Em uma expedição à Lua, onde g = 1,6m/s², a massa desse astronauta será igual a?

MEDIDA DE UMA FORÇA

Podemos medir a intensidade de uma força pela deformação que ela produz num corpo.

O dispositivo utilizado é o dinamômetro que consiste numa mola helicoidal de aço envolvida por um protetor. Na extremidade livre da mola há um ponteiro que se desloca ao longo de uma escala.

A medida de uma força é feita por comparação da deformação causada por essa força com a de forças padrão.

FORÇA ELÁSTICA ou LEI DE HOOKE

Imagine uma mola presa em uma das extremidades a um suporte, e em estado de repouso (sem ação de nenhuma força).

Quando aplicamos uma força F na outra extremidade, a mola tende a deformar (esticar ou comprimir, dependendo do sentido da força aplicada).

Ao estudar as deformações de molas e as forças aplicadas, Robert Hooke (1635-1703), verificou que a deformação da mola aumenta proporcionalmente à força. Daí estabeleceu-se a seguinte lei, chamada Lei de Hooke:

Onde:
F: intensidade da força aplicada (N);
k: constante elástica da mola (N/m);
x: deformação da mola (m).

A constante elástica da mola depende principalmente da natureza do material de fabricação da mola e de suas dimensões. Sua unidade mais usual é o N/m (newton por metro) mas também encontramos N/cm; kgf/m, etc.

Exemplo:

1) Um bloco de 7,5kg, em equilíbrio, está preso a uma das extremidades de uma mola, cuja constante elástica é de 150N/m. Determine a deformação sofrida pela mola, considerando g = 10m/s².

FORÇA DE ATRITO

A força de atrito sempre se opõe à tendência do movimento do corpo sobre a superfície e é decorrente, dentre outros fatores, da existência de pequenas irregularidades da superfície em contato.

Atrito Estático: A força de atrito estático que atua sobre um corpo é variável, estando sempre a equilibrar as forças que tendem a colocar o corpo em movimento.

A força de atrito estático cresce até um valor máximo. Este valor máximo é dado por Fat= μe.|P|, onde μe é o coeficiente de atrito estático entre as superfícies e |P| é o modulo da força peso.

Atrito Cinético ou Dinâmico: Quando a força aplicada for maior que a força de atrito.

FORÇA CENTRÍPETA

Quando um corpo efetua um Movimento Circular, este sofre uma aceleração que é responsável pela mudança da direção do movimento, a qual chamamos aceleração centrípeta.

Sabendo que existe uma aceleração e sendo dada a massa do corpo, podemos, pela 2ª Lei de Newton, calcular uma força que assim como a aceleração centrípeta, aponta para o centro da trajetória circular.

A esta força damos o nome de Força Centrípeta. Sem ela, um corpo não poderia executar um movimento circular. A aceleração centrípeta é constante, logo, a força centrípeta também é constante.

Sabendo que:

A força centrípeta é a resultante das forças que agem sobre o corpo, com direção perpendicular à trajetória.

Exemplo:

1) Um carro percorre uma curva de raio 100m, com velocidade 20m/s. Sendo a massa do carro 800kg, qual é a intensidade da força centrípeta?

LOOPING

No looping, um carrinho de montanha-russa está sujeito a uma resultante centrípeta.

Exemplo:

1) Um motociclista realiza um movimento circular num plano vertical dentro de um "globo da morte" de raio 4,9m. Determine o menor valor da velocidade no ponto mais alto para a moto não perder o contato com o globo. Adote g = 10m/s².

PRINCÍPIO DA AÇÃO E REAÇÃO OU 3° LEI DE NEWTON

Quando dois corpos interagem aparece um par de forças como resultado da ação qu um corpo exerce sobre o outro. Essas forças são comumente chamadas de ação e reação.

O princípio da ação e reação estabelece as seguintes propriedades das forças decorren tes de uma interação entre os corpos:

A toda ação corresponde uma reação, com a mesma intensidade, mesma direção e sentido contrário.

Admita dois patinadores, A e B. Se A exerce uma força F_A em B, este, simultaneamente reage e exerce uma força F_B em A.

Pela 3° lei de Newton, as forças de ação e reação apresentam:

mesma intensidade: F_A = F_B
mesma direção: horizontal
sentidos contrários: F_A = - F_B (o sinal - indica que são forças de sentidos opostos)

A seguir, mostramos exemplos importantes da aplicação do princípio da ação e reação.

Apresentamos também o par de forças ação-reação em alguns exemplos:

a) Força peso — Na interação da Terra com um corpo, o peso do corpo é a ação, e a força que o corpo exerce sobre a Terra é a reação.

b) Força de tração em fio — Quando esticamos um fio ideal (inextensível e de massa desprezível) , nas suas extremidades aparecem forças de mesma intensidade chamadas forças de tração (T).

c) Força de reação normal — Um corpo em repouso, apoiado numa superfície horizontal, aplica sobre esta uma força F de compressão, cuja intensidade é igual à do seu peso. A superfície de apoio exerce no corpo uma força N de reação, que por ser perpendicular às superfícies de contato é chamada força de reação normal de apoio.

Ao considerarmos o peso do corpo, nele atuam duas forças de mesma intensidade e sentidos contrários. Logo, elas se anulam.

APLICAÇÕES DAS LEIS DE NEWTON

Vamos ver agora algumas aplicações das Leis de Newton.

PLANO INCLINADO

Dadas duas trajetórias abaixo, em qual delas é "mais fácil" carregar o bloco?

Obviamente, na trajetória inclinada, pois no primeiro caso, teremos que realizar uma força que seja maior que o peso do corpo. Já no segundo caso, devemos fazer uma força que seja maior que uma das componentes de seu peso, neste caso, a componente horizontal, que terá intensidade menor conforme o ângulo formado for menor.

Por isso, no nosso cotidiano, usamos muito o plano inclinado para facilitar certas tarefas.

Ao analisarmos as forças que atuam sobre um corpo em um plano inclinado, temos:

A força Peso e a força Normal, neste caso, não tem a mesma direção pois, como já vimos, a força Peso, é causada pela aceleração da gravidade, que tem origem no centro da Terra, logo a força Peso têm sempre direção vertical.

Já a força Normal é a força de reação, e têm origem na superfície onde o movimento ocorre, logo tem um ângulo igual ao plano do movimento.

Para que seja possível realizar este cálculo devemos estabelecer algumas relações:

Podemos definir o plano cartesiano com inclinação igual ao plano inclinado, ou seja, com o eixo x formando um ângulo igual ao do plano, e o eixo y, perpendicular ao eixo x;

A força Normal será igual à decomposição da força Peso no eixo y;

A decomposição da força Peso no eixo x será a responsável pelo deslocamento do bloco;

O ângulo formado entre a força Peso e a sua decomposição no eixo y, será igual ao ângulo formado entre o plano e a horizontal;

Se houver força de atrito, esta se oporá ao movimento, neste caso, apontará para cima.

Sabendo isto podemos dividir as resultantes da força em cada direção:

Exemplo:

1) Um corpo de massa 12kg é abandonado sobre um plano inclinado formando 30° com a horizontal. O coeficiente de atrito dinâmico entre o bloco e o plano é 0,2. Qual é a aceleração do bloco?

SISTEMA DE BLOCOS

Agora que conhecemos os princípios da dinâmica, a força peso, elástica, centrípeta, de atito e o plano inclinado, podemos calcular fenômenos físicos onde estas forças são combinadas.

Corpos em contato Quando uma força é aplicada a corpos em contato, existem "pares ação-reação" de forças que atuam entre eles e que se anulam.

Podemos fazer os cálculos neste caso, imaginando:

Depois de sabermos a aceleração, que é igual para ambos os blocos, podemos calcular as forças que atuam entre eles, utilizando a relação que fizemos acima:

F_BA = m_B.a
Exemplo:

1) Sendo m_A = 5kg e m_B = 3kg, e que a força aplicada ao sistema é de 24N, qual é a intensidade da força que atua entre os dois blocos?

Corpos ligados por um fio ideal

Um fio ideal é caracterizado por ter massa desprezível, ser inextensível e flexível, ou seja, é capaz de transmitir totalmente a força aplicada nele de uma extremidade à outra.

Como o fio ideal tem capacidade de transmitir integralmente a força aplicada em sua extremidade, podemos tratar o sistema como se os corpos estivessem encostados:

A tração no fio será calculada através da relação feita acima:

T = m_B.a
Exemplo:

1) Dois blocos A e B, de massas 2,0kg e 6,0kg, respectivamente, e ligados por um fio, estão em repouso sobre um plano horizontal. Quando puxado para a direita pela força F mostrada na figura, o conjunto adquire aceleração de 2m/s².

Nestas condições, pode-se afirmar que o módulo da resultante das forças que atuam em A e o módulo da resultante das forças que atuam em B valem, em newtons, respectivamente:

Corpos ligados por um fio ideal através de polia ideal

Uma polia ideal tem a capacidade de mudar a direção do fio e transmitir a força integralmente.

Como as forças Peso e Normal no bloco A se anulam, é fácil verificar que as forças que causam o movimento são a Tração e o Peso do Bloco B.

Conhecendo a aceleração do sistema podemos calcular a Tensão no fio:

T = m_A.a
Exemplo:

1) Na figura abaixo temos dois blocos que estão ligados entre si por uma corda ideal, isto é, cuja massa é desprezível. Podemos ver que o bloco A encontrasse apoiado sobre uma superfície plana. Adote m_A = 9kg e m_B = 6kg, determine o valor da tração na corda.

2) Uma máquina de Atwood possui massas m_A = 6,25kg e m_B = 6,75kg ligadas por uma corda ideal, inextensível e de massa desprezível, através de uma polia também ideal. Determinar:

a) A aceleração do sistema;
b) A tensão na corda que liga as massas;
c) A tensão na corda que prende o sistema ao teto.

Corpo preso a uma mola

Então, conforme a 2ª Lei de Newton:

F - P = m.a
Mas F = k.x e P = m.g, então:
k.x - m.g = m.a
Assim poderemos calcular o que for pedido, se conhecermos as outras incógnitas.

TRABALHO DE UMA FORÇA (W)

A quantidade de energia adquirida ou transferida por um corpo pode ser medida pela grandeza chamada trabalho de uma força. Trata-se de uma grandeza escalar (positiva ou negativa) que mede o efeito da ação de uma força sobre um corpo ao longo de um deslocamento. Basicamente, o trabalho indica se a força, atuando sozinha, contribui para acelerar o corpo (com ganho de energia) ou para retardar o corpo (com perda de energia).

TRABALHO DE UMA FORÇA CONSTANTE

Vimos que o trabalho de uma força que atua sobre um corpo em movimento depende do deslocamento ΔS sofrido pelo corpo, da intensidade da força aplicada e do ângulo θ que essa força forma com a direção do deslocamento.

Então, o trabalho de uma força com intensidade constante é definido:

No SI, a unidade de medida de trabalho é: N.m = J (Joule).

Em relação ao ângulo θ, podemos ter as situações a seguir.

1°) 0° ≤ θ < 90°: O valor de cosθ é positivo, e o trabalho realizado pela força também é positivo. Então, o trabalho é denominado trabalho motor.

2°) θ = 90°: O valor de cosθ é zero, e não há realização de trabalho. Nesse caso, o trabalho da força F é denominado trabalho nulo e indica que a força não gera deslocamento.

3°) 90° < θ ≤ 180°: O valor de cosθ é negativo, e o trabalho realizado pela força também é negativo. Nesse caso, o trabalho é denominado trabalho resistente.

Exemplos:

1) Um corpo A se desloca 10m em um plano horizontal sob a ação das forças F₁, F₂, F₃ e F₄, de acordo com a figura abaixo. Sabendo que as forças têm mesma intensidade, de valor 20N, e que formam, respectivamente, os ângulos θ₁, θ₂, θ₃ e θ₄ com direção do deslocamento, calcule o trabalho realizado por cada força.
Dados:
θ₁ = 0° e cos 0° = 1.
θ₂ = 60° e cos 60° = 0,5.
θ₃ = 90° e cos 90° = 0.
θ₄ = 120° e cos 120° = - 0,5.

Resolução:

2) Um corpo de 2kg de massa é lançado em um chão áspero, com velocidade inicial de 4m/s, e percorre uma distância de 4m até parar. Considerando a aceleração constante, determine:
a) a aceleração escalar do corpo;
b) o módulo da força de atrito;
c) o trabalho realizado pela força de atrito.

TRABALHO DE UMA FORÇA VARIÁVEL

Agora vamos estudar o trabalho realizado por uma força cuja intensidade varia ao longo do deslocamento.

A figura acima nos mostra a representação gráfica da força aplicada em função do deslocamento.

Na figura, o trabalho realizado pela força variável é dado numericamente igual à área da figura determinada pela linha vermelha do gráfico com o eixo horizontal, dentro do intervalo de tempo considerado.

Ou seja, para calcular o trabalho realizado por uma força variável basta calcular a área da figura.

POTÊNCIA

Potência é a grandeza escalar que mede a rapidez com que determinado trabalho é realizado.

Considere uma força que realiza um trabalho T num intervalo de tempo ∆t. Supondo que o trabalho seja diretamente proporcional ao intervalo de tempo de tempo, a potência da força é igual ao quociente entre o trabalho e o intervalo de tempo:

No sistema Internacional, a potência é medida em Watt (W): 1 W = 1 J/s

Outras duas unidades muito utilizadas quando se fala em potência é:

Horse-Power (HP): 1HP = 745,7W
Cavalo-Vapor (VC): 1VC = 735,5W

Observação: Se o trabalho não for diretamente proporcional ao intervalo de tempo, o quociente T/∆t representará a potência média da força no intervalo de tempo considerado.

Exemplos:

1) Calcule a potência média de uma força que produz um trabalho de 300 J em 10 s.

2) Um motor de 50 kW de potência aciona um veículo durante uma hora. Qual o trabalho desenvolvido pelo motor?

Relação entre potência e velocidade

A potência também pode ser calculada em função da força que realiza trabalho e da velocidade de seu ponto de aplicação. Sendo F uma força que se move com velocidade V, paralela a F, a potência média num certo intervalo de tempo ∆t é:

Mas, nesse caso, T = F.d, pois V é paralelo a F. Logo:

A velocidade média é v = d/∆t. Portanto:

Esse resultado também é válido para um determinado instante. Nesse caso, v é a velocidade instantânea e P, a Potência instantânea.

RENDIMENTO OU EFICIÊNCIA (η)

Uma máquina sempre deve receber energia a uma determinada taxa, para poder operar – isso é potência total (Pot_T). Normalmente nem toda a potência é aproveitada para a execução de um trabalho útil. Em uma lâmpada, grande parte da potência total é utilizada para iluminar o ambiente (potência útil), e o restante se perde sob a forma de calor (potência dissipada). Nesse caso, dizemos que a fração do total utilizada para conversão em parte útil é o rendimento (η) do dispositivo.

Como se relacionam essas parcelas?
Pot_T = Pot_u + Pot_d

O rendimento ou eficiência de uma máquina ou um sistema físico é a medida do aproveitamento da potência total recebida, sendo a razão entre as potências útil e total:

Note que o rendimento é uma grandeza adimensional (não tem unidade de medida). Frequentemente indica-se o rendimento percentual η%, multiplicando-se η por 100:

η% = 100.η , 0 ≤ η% ≤ 100%.

Exemplos:

1) Uma máquina tem potência total de 500HP e rendimento de 60%. Determine:
a) a potência útil que ela desenvolve;

b) o trabalho útil que sua força pode realizar em 10s.

REFERENCIAL TEÓRICO

MÁXIMO, Antônio; ALVARENGA, Beatriz. Física: Ensino Médio, Volume Único, 2012.
GASPAR, Alberto. Física, Volume Único, 2011.
BONJORNO, José Alberto; BONJORNO, Regina Azenha; BONJORNO, Valter; CLINTON, Márcico Ramos. Física: Fundamental, Volume Único , 2006.
BONJORNO, José Alberto; BONJORNO, Regina de Fátima Souza Azenha; BONJORNO, Valter; BONJORNO, Mariza Azzolini; CLINTON, Márcico Ramos; EDUARDO PRADO, de Pinho; CASEMIRO, Renato. Física: Mecânica, V. 1, 2016.
GASPAR, Alberto. Física: Série Brasil, Ensino Médio/Volume Único, 2006, Ed. Ática.